Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, x6, x7, x8, которые удовлетворяют указанному ниже условию?
((x1 → x2) → (x3 → x4)) & ((x3 → x4) → (x5 → x6)) & ((x5 → x6) → (x7 → x8)) = 1
Обозначим:
А=(x1 → x2)
B=(x3 → x4)
C=(x5 → x6)
D=(x7 → x8)
Получим систему логических уравнений:
A → B =1
B → C =1
C → D =1
Система логических уравнений имеет решения:
A B C D
0 0 0 0
0 0 1 0
0 0 1 1
0 1 1 1
1 1 1 1
Всего 5 решений.
Вернёмся к x1, x2 … x8:
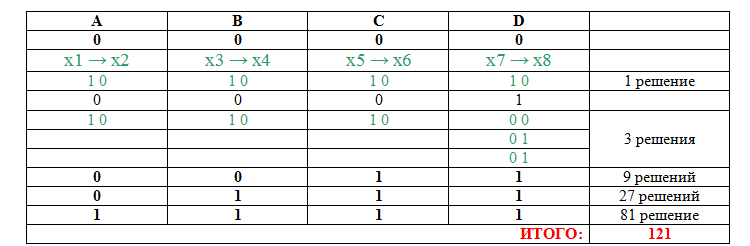
Ответ: 121.
